Introduction

Let C(M,N) be the space of smooth maps phi: (M,g)–>(N,h) between two Riemannian manifolds. A map phi in C(M,N) is called harmonic if it is a critical point of the energy functional

and is characterized by the vanishing of the tension field tau(phi)=trace\nabla d(phi).

In the same vein, if we denote by Imm(M,N) the space of Riemannian immersions in (N,h), then a Riemannian immersion phi: (M,phi^*h)–>(N,h) is called minimal if it is a critical point of the volume functional

and the corresponding Euler-Lagrange equation is H=0, where H is the mean curvature vector field.

If phi: (M,g)–>(N,h) is a Riemannian immersion, then it is a critical point of the energy in C(M,N) if and only if it is a minimal immersion. Thus, in order to study minimal immersions one can look at harmonic Riemannian immersions.

A natural generalization of harmonic maps and minimal immersions can be given by considering the functionals obtained integrating the square of the norm of the tension field or of the mean curvature vector field, respectively. More precisely:

• biharmonic maps are the critical points of the bienergy functional

  

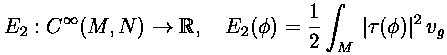
• Willmore immersions are the critical points of the Willmore functional

  

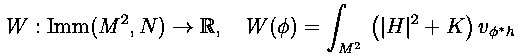
  where K is the sectional curvature of (N,h) restricted to the image of M².

While the above variational problems are natural generalizations of harmonic maps and minimal immersions, biharmonic Riemannian immersions do not recover Willmore immersions, even when the ambient space is Rⁿ. Therefore, the two generalizations give rise to different variational problems.

In a different setting, B.Y. Chen defined biharmonic submanifolds M of the Euclidean space as those with harmonic mean curvature vector field, that is Delta H =0, where Delta is the rough Laplacian. If we apply the definition of biharmonic maps to Riemannian immersions into the Euclidean space we recover Chen’s notion of biharmonic submanifolds. Thus biharmonic Riemannian immersions can also be thought as a generalization of Chen’s biharmonic submanifolds.

An alternative option for bienergy is to compose a map (often just taken in L²) between Riemannian manifolds, with an Riemannian immersion of the target into a large-enough Euclidean space, as granted by Nash Theorem, and consider the (intrinsic) bienergy, as defined above, of this vector-valued map.
Critical points of this functional, for variations through maps into the original target manifold, are called extrinsic biharmonic maps.
Contrary to the case of harmonic maps, the intrinsic and extrinsic approaches do not coincide.

In the last decade there has been a growing interest in the theory of biharmonic maps which can be divided in two main research directions. On the one side, the differential geometric aspect has driven attention to the construction of examples and classification results. The other side is the analytic aspect from the point of view of PDE: biharmonic maps are solutions of a fourth order strongly elliptic semilinear PDE.

Extrinsic biharmonic maps have essentially been studied for their analytical properties: regularity of weak solutions; monotony formulas; study of the flow. Probably due to this analytical nature, their geometrical properties and interactions with (intrinsic) biharmonic maps remain unknown.

The differential geometric aspect of biharmonic submanifolds was also studied in the semi-Riemannian case, which is very rich in examples.

We mention some other reasons that should encourage the study of biharmonic maps.

• The theory of biharmonic functions is an old and rich subject: they have been studied since 1862 by Maxwell and Airy to describe a mathematical model of elasticity; the theory of polyharmonic functions was later on developed, for example, by E. Almansi, T. Levi-Civita and M. Nicolescu. More recently, biharmonic functions on Riemannian manifolds were studied, among others, by R. Caddeo, T. Hangan, L. Sario and L. Vanhecke.

• The identity map of a Riemannian manifold is trivially a harmonic map, but in most cases is not stable (local minimum), for example consider Sⁿ, n>2. In contrast, the identity map, as a biharmonic map, is always stable, in fact an absolute minimum of the energy.

• Harmonic maps do not always exist, for instance, J. Eells and J.C. Wood showed that there exists no harmonic map from T² to S² (whatever the metrics chosen) in the homotopy class of Brower degree +/- 1. We expect biharmonic maps to succeed where harmonic maps failed.